Class 7 Algebraic Expressions Worksheet – Simplification and Expansion

Master algebraic expressions for Class 7 with this worksheet - monomials, binomials, trinomials, and expansion of brackets. Includes solved examples and practice problems to help your child simplify, multiply, and evaluate expressions with confidence.

What are Algebraic Expressions?

An algebraic expression is a combination of numbers, variables, and operations. At Class 7, we work with expressions that have multiple variables, exponents, and brackets that need expanding.

The focus shifts from simply identifying terms to manipulating expressions — adding, subtracting, multiplying, and dividing them, then simplifying the result. Understanding how to handle signs inside brackets and combine like terms correctly is the foundation of everything that follows in algebra.

Key Definitions

Monomial: An expression with a single term, like 5x or −3y².

Binomial: An expression with exactly two terms, like 3x + 5 or a² − 4b.

Trinomial: An expression with exactly three terms, like x² + 2x + 1.

Degree: The highest power of the variable in an expression. In 5x³ + 2x² − 7x + 3, the degree is 3.

Rules for Operations

Like terms are terms that have the same variables raised to the same powers. Only like terms can be combined. For example, 3xy and 5xy are like terms, but 5xy and 5x are not.

When expanding brackets, multiply the term outside by every term inside. So 3(2x + 5 − 1) requires three separate multiplications.

When a negative sign sits before a bracket, it flips the sign of every term inside. This is where most mistakes happen.

When multiplying powers of the same base, add the exponents: x² × x³ = x⁵.

Solved Example

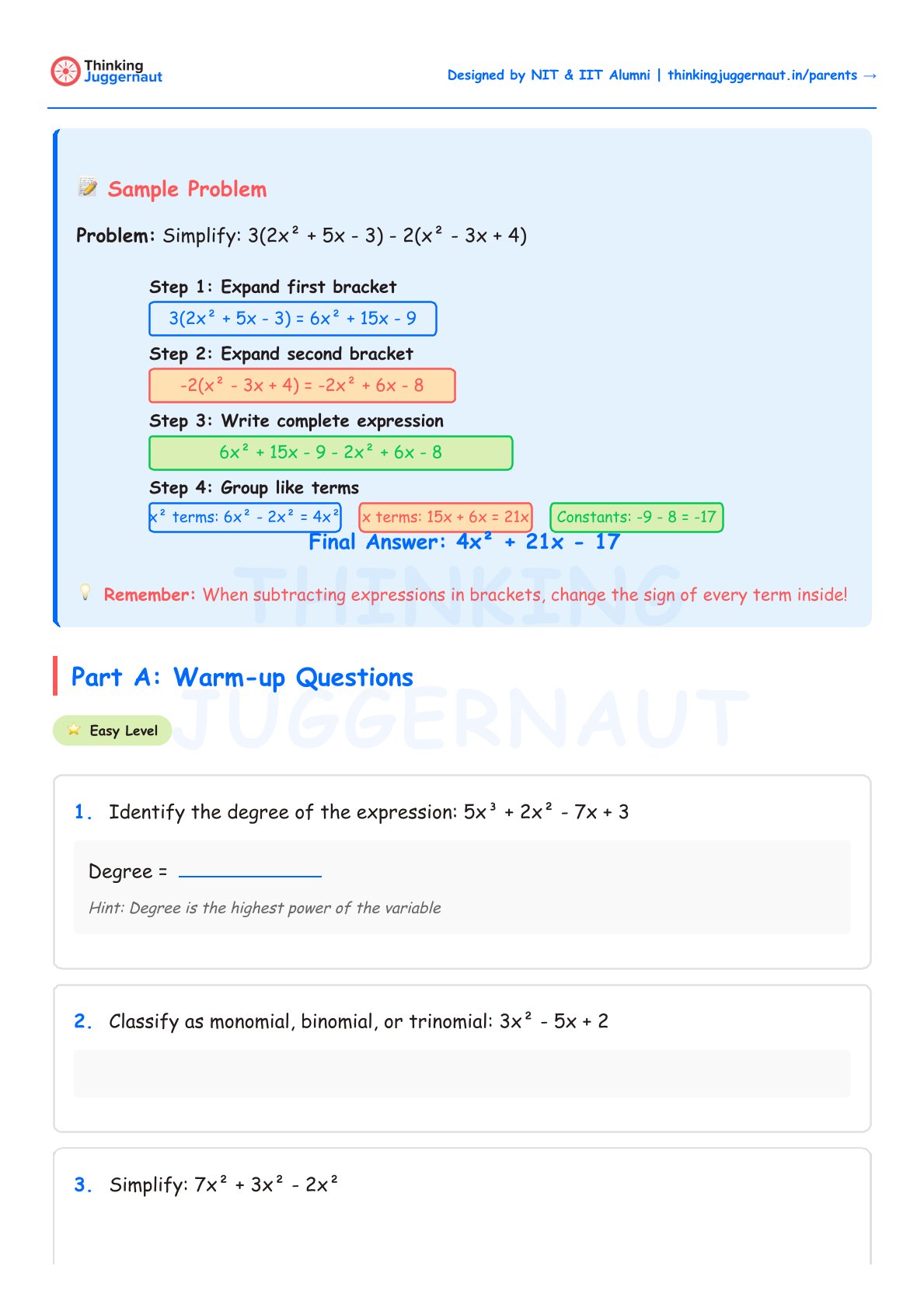
Simplify: 3(2x² + 5x − 3) − 2(x² − 3x + 4)

Step-by-Step Solution

Expand the first bracket: 3 × 2x² = 6x², 3 × 5x = 15x, 3 × (−3) = −9. This gives 6x² + 15x − 9.

Expand the second bracket, remembering the negative sign in front flips all signs inside: −2 × x² = −2x², −2 × (−3x) = +6x, −2 × 4 = −8. This gives −2x² + 6x − 8.

Write the full expression: 6x² + 15x − 9 − 2x² + 6x − 8.

Group and combine like terms. The x² terms: 6x² − 2x² = 4x². The x terms: 15x + 6x = 21x. The constants: −9 − 8 = −17.

Answer: 4x² + 21x − 17.

Practice Problems

• Simplify 5x² + 3xy − 2x² + 7xy − 4 by grouping and combining like terms. → Combining Like Terms with Multiple Variables
• Expand and simplify 4(2x + 3y) − 3(x − 2y). → Expanding Two Brackets and Simplifying
• The area of a rectangle is (6x² + 9x) cm² and the length is 3x cm. Find an expression for the breadth. → Dividing Polynomials in a Geometry Context
• If a = 3 and b = −2, evaluate 2a² − 3ab + b². → Substituting Values into an Expression
• Priya scores x marks in Math, (x + 15) in Science, and (x − 5) in English. Write and simplify an expression for her total marks. → Building and Simplifying Expressions from Word Problems
• A polynomial P(x) = ax² + bx + c satisfies P(0) = 5, P(1) = 8, and P(2) = 13. Find a, b, and c. → Finding Coefficients Using Given Conditions

Scoring Guide

• 20–24 marks: Excellent! You have mastered algebraic expressions. Challenge yourself with factorisation and algebraic identities next.
• 15–19 marks: Very Good! Practice problems with multiple brackets and complex simplifications. Pay close attention to sign changes.
• 10–14 marks: Good Effort! Focus on expanding brackets correctly. Practice with single brackets first before moving to two or more.
• 0–9 marks: Keep Trying! Review basic addition and subtraction of polynomials. Practice identifying like terms before attempting simplification.

Tips and Common Mistakes

The negative sign before a bracket changes the sign of every single term inside. So −(3x − 2) becomes −3x + 2, not −3x − 2. This is the most frequent error at this level and it affects every subsequent step.

x² and x are not like terms. They have different powers and cannot be combined. Treating them as like terms is a common mistake that leads to wrong simplification.

When multiplying terms like 2x × 3x, multiply the numbers and add the powers separately. The result is 6x², not 6x.

When expanding a bracket with three or more terms inside, distribute to every single term. Missing one term changes the entire expression.

After simplifying, arrange terms in descending order of power. This makes expressions easier to read and compare, and helps catch errors.

Always substitute a simple value like x = 1 or x = 0 back into both the original and simplified expressions to check if they give the same result. This is the quickest way to verify your work.