Class 8 Algebraic Expressions & Identities Worksheet – Factorisation and Expansion

Algebraic identities and factorisation worksheet for Class 8: Expansion, common factors, regrouping, and sum/difference of cubes. Includes solved examples and challenging problems to build advanced algebra skills.

What are Algebraic Expressions and Identities?

At Class 8, algebra moves from solving equations to manipulating and factorising expressions. We now work with a larger set of identities — including cubic identities and three-variable expansions — and learn to factorise expressions by recognising patterns rather than trial and error.

Factorisation is essentially expansion in reverse: instead of multiplying out brackets, we break an expression back into its factors. The ability to spot which identity applies to a given expression is the core skill at this level.

Factorisation Methods

Common Factor Method: Pull out the highest common factor shared by every term. For example, 12x² + 18x becomes 6x(2x + 3).

Regrouping Method: When there is no single common factor across all terms, group them in pairs, take out a common factor from each pair, then factorise the shared bracket.

Using Identities: Recognise the expression as a known pattern — perfect square, difference of squares, sum or difference of cubes — and write it in factored form directly.

Standard Identities at This Level

The Class 7 identities still apply: (a + b)², (a − b)², (a + b)(a − b), and (x + a)(x + b). Class 8 adds three new ones: (a + b + c)² for three-variable expansions, (a + b)³ and (a − b)³ for cubic expansions, and a³ + b³ and a³ − b³ for factorising sum and difference of cubes.

Solved Example

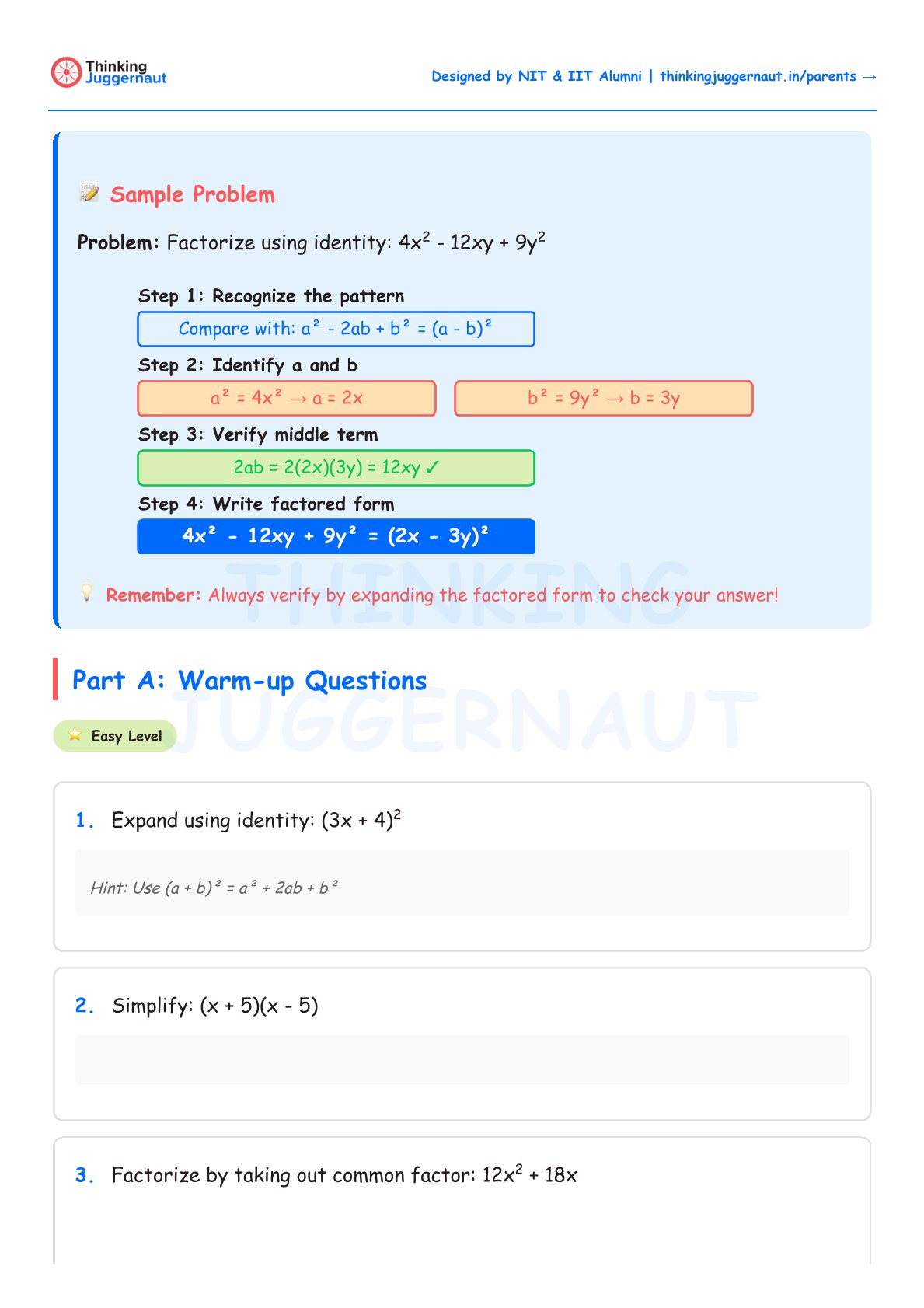
Factorise: 4x² − 12xy + 9y²

Step-by-Step Solution

First, compare the expression with the known identity (a − b)² = a² − 2ab + b². This works when the first and last terms are perfect squares and the middle term is negative.

Identify a and b. Since a² = 4x², we get a = 2x. Since b² = 9y², we get b = 3y.

Verify the middle term. The identity requires 2ab = 2(2x)(3y) = 12xy. The expression has −12xy, which matches the negative sign in (a − b)².

Write the factored form: 4x² − 12xy + 9y² = (2x − 3y)².

Always verify by expanding (2x − 3y)² back out to confirm it gives the original expression.

Practice Problems

• Factorize x² + 10x + 25 by recognising it as a perfect square identity. → Recognising Perfect Square Trinomials
• Expand (2x + 3y + 4z)² using the three-variable identity and simplify. → Applying the Three-Variable Expansion
• Factorize ax + ay + bx + by by regrouping into pairs. → Regrouping Method
• Evaluate 103² without long multiplication, using the identity (100 + 3)². → Using Identities for Mental Arithmetic
• The area of a square is (4x² + 12x + 9) cm². Find the length of its side by factorising. → Geometry Problem Using Perfect Square Identity
• Factorize x⁴ − 16 completely, applying difference of squares twice. → Multi-step Factorisation

Scoring Guide

• 20–24 marks: Excellent! You have mastered algebraic identities and factorisation. Move on to quadratic equations and polynomial division.
• 15–19 marks: Very Good! Practice cubic identities and complex factorisation problems to strengthen your skills further.
• 10–14 marks: Good Effort! Focus on memorising all identities and learning to recognise patterns before attempting factorisation.
• 0–9 marks: Keep Trying! Review the identities section thoroughly. Practice basic expansions and simple factorisations daily before tackling harder problems.

Tips and Common Mistakes

Recognising the pattern is more important than memorising every identity. Before applying any identity, check whether the first and last terms are perfect squares. If they are, the expression is likely a perfect square trinomial or difference of squares.

The identity (a − b)² is not the same as a² − b². The middle term 2ab is critical. Confusing these two is the most persistent error at this level and it carries forward into every factorisation problem.

Always take out common factors first before trying to apply an identity. If every term shares a factor, pull it out first. Trying to match an identity without doing this step leads to unnecessary confusion.

Factorisation is not always complete after one step. For example, x⁴ − 16 first becomes (x² − 4)(x² + 4), but x² − 4 can be factorised again into (x − 2)(x + 2). Always check whether any factor can be broken down further.

When using identities for mental arithmetic — like calculating 103² as (100 + 3)² — write out each term of the expansion separately before adding. Trying to do it all in one step leads to errors.

Verify every factorisation by expanding the answer back out. If it matches the original expression, the factorisation is correct. This takes only a few seconds and prevents mistakes from going unnoticed.